(5.) Determine the polynomial function whose
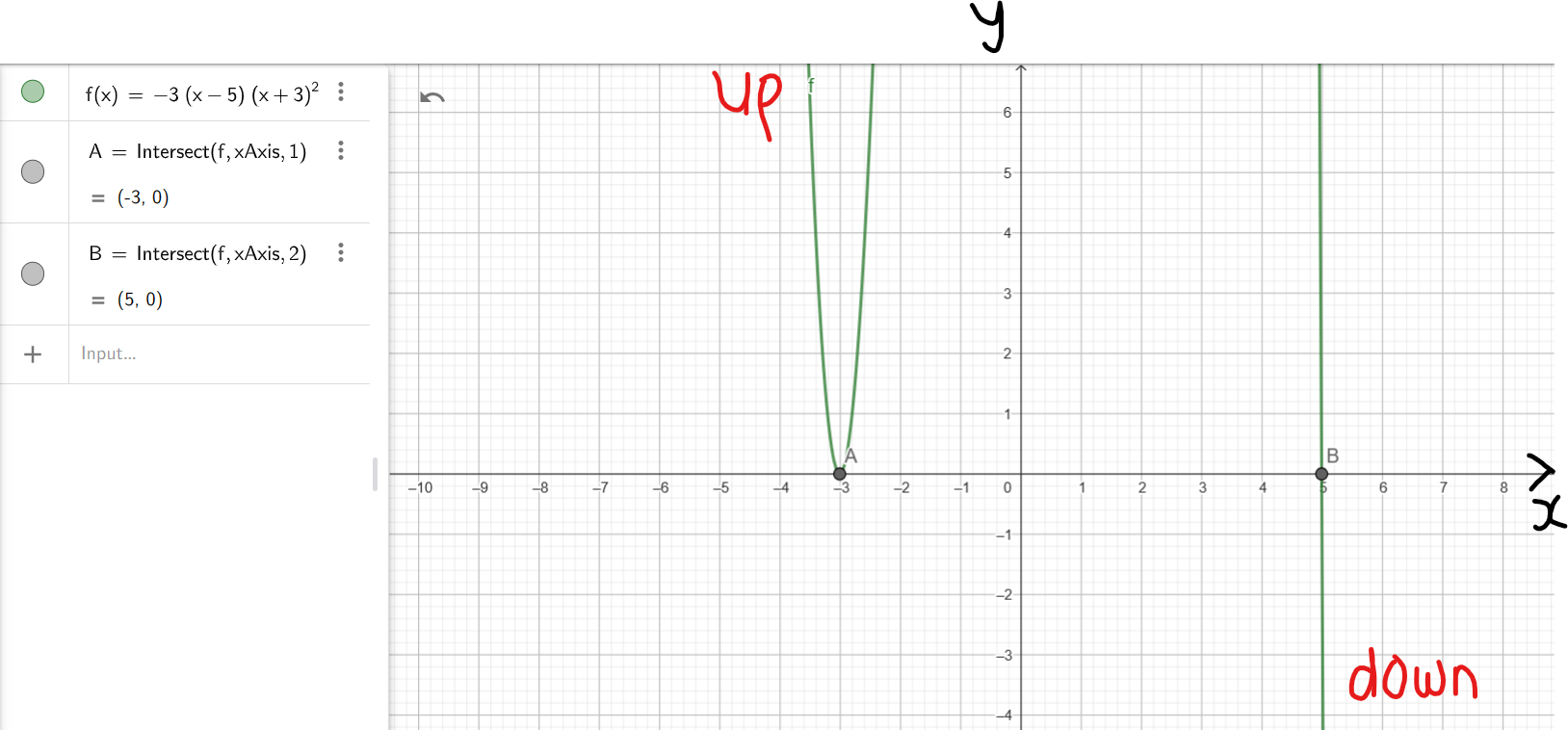
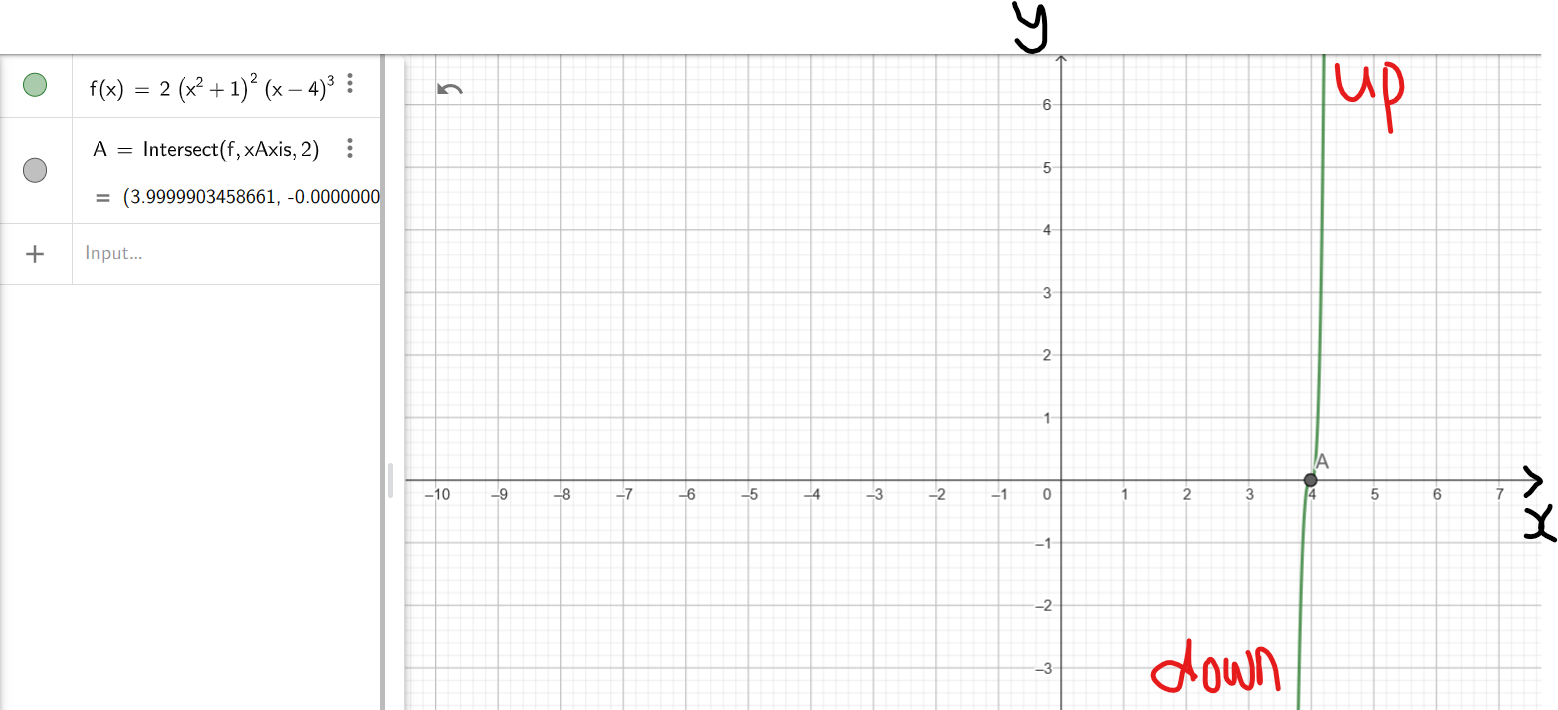
(a.) zeros are: −3, 2, 5 and whose graph passes through the point (6, 72)
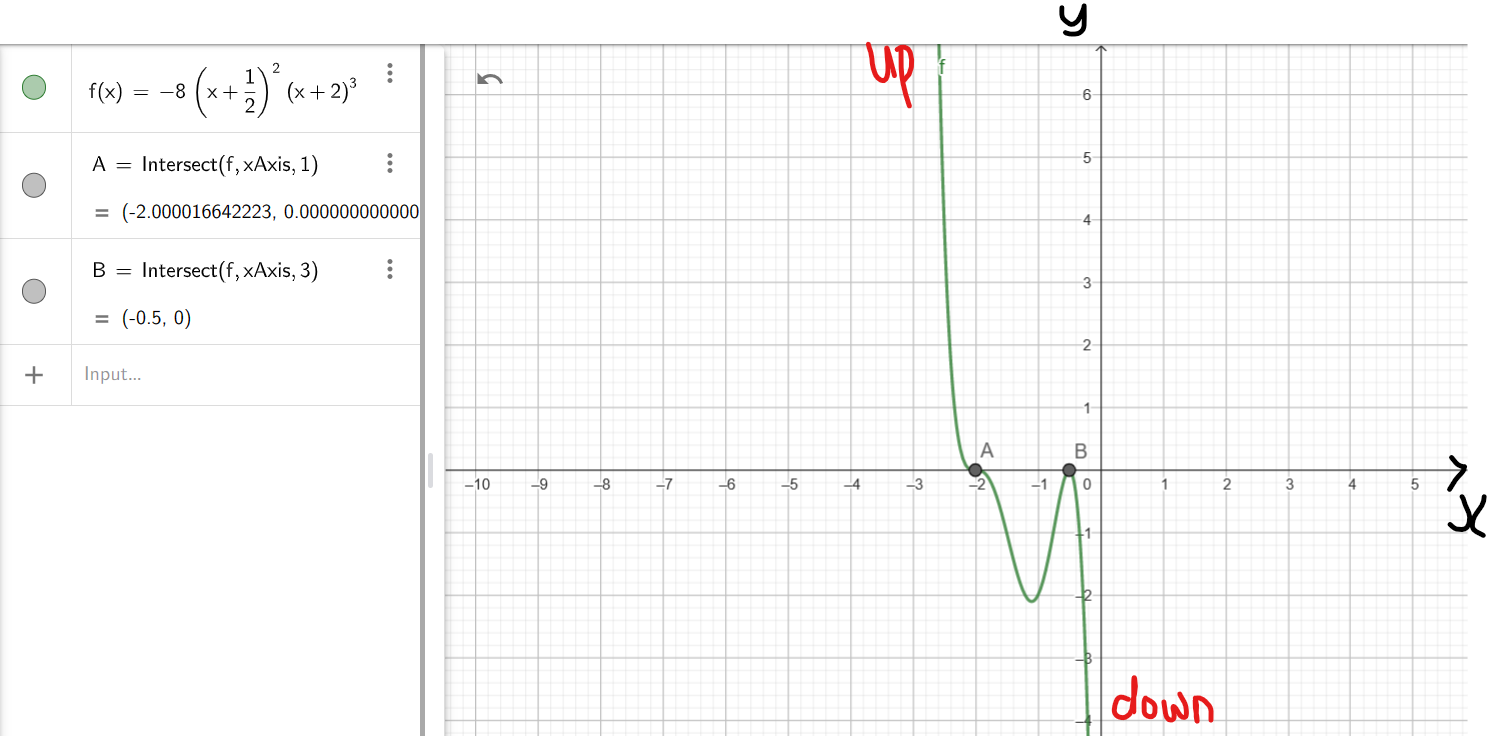
(b.) zeros are: −2, multiplicity 2; 2, multiplicity 2; and degree is: 4 and whose graph passes through the point (−3, 125)
$ (a.) \\[3ex] zeros = -3, 2, 5 \\[3ex] factors = (x + 3)(x - 2)(x - 5) \\[3ex] \implies \\[3ex] f(x) = a(x + 3)(x - 2)(x - 5) \\[3ex] passes\;\;through\;\;(6, 72) \\[3ex] To\;\;find\;\;leading\;\;coefficient:a \\[3ex] x = 6,\;\;\;f(x) = 72 \\[3ex] \implies \\[3ex] 72 = a(6 + 3)(6 - 2)(6 - 5) \\[3ex] 72 = a(9)(4)(1) \\[3ex] 36a = 72 \\[3ex] a = \dfrac{72}{36} \\[5ex] a = 2 \\[3ex] \implies \\[3ex] f(x) = a(x + 3)(x - 2)(x - 5) \\[3ex] = 2(x + 3)(x - 2)(x - 5) \\[3ex] = (2x + 6)(x^2 - 5x - 2x + 10) \\[3ex] = (2x + 6)(x^2 - 7x + 10) \\[3ex] = 2x^3 - 14x^2 + 20x + 6x^2 - 42x + 60 \\[3ex] = 2x^3 - 8x^2 - 22x + 60 \\[3ex] (b.) \\[3ex] degree = 4 \\[3ex] zeros = -2, -2, 2, 2 \\[3ex] factors = (x + 2)(x + 2)(x - 2)(x - 2) \\[3ex] factors = (x + 2)(x - 2)(x + 2)(x - 2) \\[3ex] (x + 2)(x - 2) = x^2 - 2^2 ...Difference\;\;of\;\;Two\;\;Squares \\[3ex] \implies \\[3ex] factors = (x^2 - 2^2)(x^2 - 2^2) \\[3ex] factors = (x^2 - 4)(x^2 - 4) \\[3ex] \implies \\[3ex] f(x) = a(x^2 - 4)(x^2 - 4) \\[3ex] passes\;\;through\;\;(-3, 125) \\[3ex] To\;\;find\;\;leading\;\;coefficient:a \\[3ex] x = -3,\;\;\;f(x) = 125 \\[3ex] \implies \\[3ex] 125 = a[(-3)^2 - 4][(-3)^2 - 4] \\[3ex] 125 = a(9 - 4)(9 - 4) \\[3ex] 125 = a(5)(5) \\[3ex] 25a = 125 \\[3ex] a = \dfrac{125}{25} = 5 \\[5ex] \implies \\[3ex] f(x) = a(x^2 - 4)(x^2 - 4) \\[3ex] = 5(x^2 - 4)(x^2 - 4) \\[3ex] = (5x^2 - 20)(x^2 - 4) \\[3ex] = 5x^4 - 20x^2 - 20x^2 + 80 \\[3ex] = 5x^4 - 40x^2 + 80 $
(a.) zeros are: −3, 2, 5 and whose graph passes through the point (6, 72)
(b.) zeros are: −2, multiplicity 2; 2, multiplicity 2; and degree is: 4 and whose graph passes through the point (−3, 125)
$ (a.) \\[3ex] zeros = -3, 2, 5 \\[3ex] factors = (x + 3)(x - 2)(x - 5) \\[3ex] \implies \\[3ex] f(x) = a(x + 3)(x - 2)(x - 5) \\[3ex] passes\;\;through\;\;(6, 72) \\[3ex] To\;\;find\;\;leading\;\;coefficient:a \\[3ex] x = 6,\;\;\;f(x) = 72 \\[3ex] \implies \\[3ex] 72 = a(6 + 3)(6 - 2)(6 - 5) \\[3ex] 72 = a(9)(4)(1) \\[3ex] 36a = 72 \\[3ex] a = \dfrac{72}{36} \\[5ex] a = 2 \\[3ex] \implies \\[3ex] f(x) = a(x + 3)(x - 2)(x - 5) \\[3ex] = 2(x + 3)(x - 2)(x - 5) \\[3ex] = (2x + 6)(x^2 - 5x - 2x + 10) \\[3ex] = (2x + 6)(x^2 - 7x + 10) \\[3ex] = 2x^3 - 14x^2 + 20x + 6x^2 - 42x + 60 \\[3ex] = 2x^3 - 8x^2 - 22x + 60 \\[3ex] (b.) \\[3ex] degree = 4 \\[3ex] zeros = -2, -2, 2, 2 \\[3ex] factors = (x + 2)(x + 2)(x - 2)(x - 2) \\[3ex] factors = (x + 2)(x - 2)(x + 2)(x - 2) \\[3ex] (x + 2)(x - 2) = x^2 - 2^2 ...Difference\;\;of\;\;Two\;\;Squares \\[3ex] \implies \\[3ex] factors = (x^2 - 2^2)(x^2 - 2^2) \\[3ex] factors = (x^2 - 4)(x^2 - 4) \\[3ex] \implies \\[3ex] f(x) = a(x^2 - 4)(x^2 - 4) \\[3ex] passes\;\;through\;\;(-3, 125) \\[3ex] To\;\;find\;\;leading\;\;coefficient:a \\[3ex] x = -3,\;\;\;f(x) = 125 \\[3ex] \implies \\[3ex] 125 = a[(-3)^2 - 4][(-3)^2 - 4] \\[3ex] 125 = a(9 - 4)(9 - 4) \\[3ex] 125 = a(5)(5) \\[3ex] 25a = 125 \\[3ex] a = \dfrac{125}{25} = 5 \\[5ex] \implies \\[3ex] f(x) = a(x^2 - 4)(x^2 - 4) \\[3ex] = 5(x^2 - 4)(x^2 - 4) \\[3ex] = (5x^2 - 20)(x^2 - 4) \\[3ex] = 5x^4 - 20x^2 - 20x^2 + 80 \\[3ex] = 5x^4 - 40x^2 + 80 $
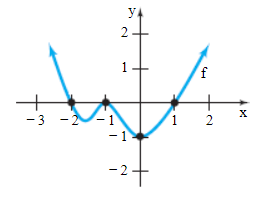
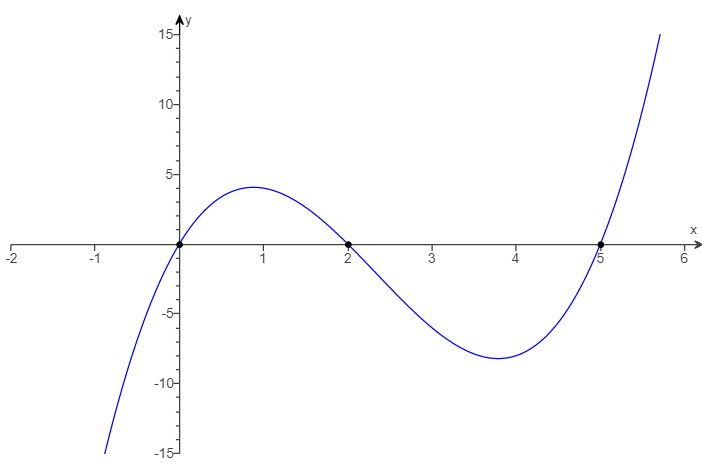
(6.) Analyze the polynomial function: $f(x) = x^2(x - 6)$
(a.) Determine the end behavior of the graph of the function.
(b.) Find the x- and y-intercepts of the graph of the function.
(c.) Determine the zeros of the function and their multiplicity.
Does the graph touch/cross the x-axis at each zero?
(d.) Determine the maximum number of turning points on the graph of the function.
(e.) Use the above information to draw a complete graph of the function.
(a.)
$f(x) = x^2(x - 6)$
Leading term = $x^2(x) = x^3$
This implies that the graph of $f(x)$ behaves like $y = x^3$ for large values of |x|
Leading coefficient = 1 (positive)
Degree = n = 3 (odd)
End behavior is: down-up
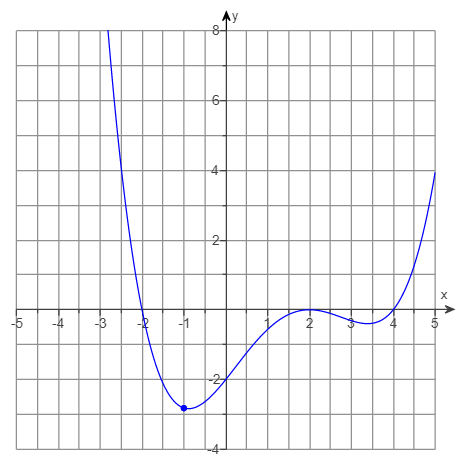
$ (b.) \\[3ex] f(x) = x^2(x - 6) \\[3ex] \underline{x-intercept} \\[3ex] x^2(x - 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; x - 6 = 0 \\[3ex] x = \sqrt{0} \;\;\;OR\;\;\; x = 6 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 6 \\[3ex] x-intercept = (0, 0),\; (0, 0),\; (6, 0) \\[3ex] \underline{y-intercept} \\[3ex] f(0) = 0^2(0 - 6) \\[3ex] f(0) = 0(-6) \\[3ex] f(0) = 0 \\[3ex] y-intercept = (0, 0) \\[3ex] (c.) \\[3ex] \underline{1st\;\;zero} \\[3ex] x = 0 \\[3ex] Multiplicity = 2\;(even) \\[3ex] Graph\;\;touches\;\;the\;\;x-axis\;\;at\;\;x = 0 \\[3ex] \underline{2nd\;\;zero} \\[3ex] x = 6 \\[3ex] Multiplicity = 1\;(odd) \\[3ex] Graph\;\;crosses\;\;the\;\;x-axis\;\;at\;\;x = 6 \\[3ex] $ (d.) The maximum number of turning points on the graph is:
= n − 1
= 3 − 1
= 2
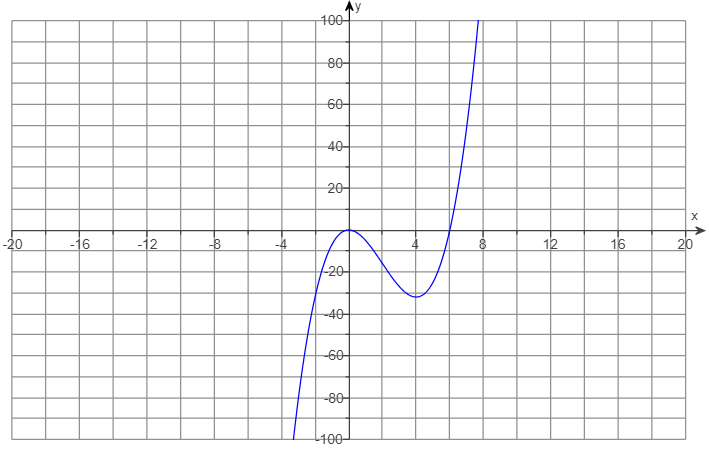
(e.) The graph of the function is:
(a.) Determine the end behavior of the graph of the function.
(b.) Find the x- and y-intercepts of the graph of the function.
(c.) Determine the zeros of the function and their multiplicity.
Does the graph touch/cross the x-axis at each zero?
(d.) Determine the maximum number of turning points on the graph of the function.
(e.) Use the above information to draw a complete graph of the function.
(a.)
$f(x) = x^2(x - 6)$
Leading term = $x^2(x) = x^3$
This implies that the graph of $f(x)$ behaves like $y = x^3$ for large values of |x|
Leading coefficient = 1 (positive)
Degree = n = 3 (odd)
End behavior is: down-up
$ (b.) \\[3ex] f(x) = x^2(x - 6) \\[3ex] \underline{x-intercept} \\[3ex] x^2(x - 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; x - 6 = 0 \\[3ex] x = \sqrt{0} \;\;\;OR\;\;\; x = 6 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 6 \\[3ex] x-intercept = (0, 0),\; (0, 0),\; (6, 0) \\[3ex] \underline{y-intercept} \\[3ex] f(0) = 0^2(0 - 6) \\[3ex] f(0) = 0(-6) \\[3ex] f(0) = 0 \\[3ex] y-intercept = (0, 0) \\[3ex] (c.) \\[3ex] \underline{1st\;\;zero} \\[3ex] x = 0 \\[3ex] Multiplicity = 2\;(even) \\[3ex] Graph\;\;touches\;\;the\;\;x-axis\;\;at\;\;x = 0 \\[3ex] \underline{2nd\;\;zero} \\[3ex] x = 6 \\[3ex] Multiplicity = 1\;(odd) \\[3ex] Graph\;\;crosses\;\;the\;\;x-axis\;\;at\;\;x = 6 \\[3ex] $ (d.) The maximum number of turning points on the graph is:
= n − 1
= 3 − 1
= 2
(e.) The graph of the function is: