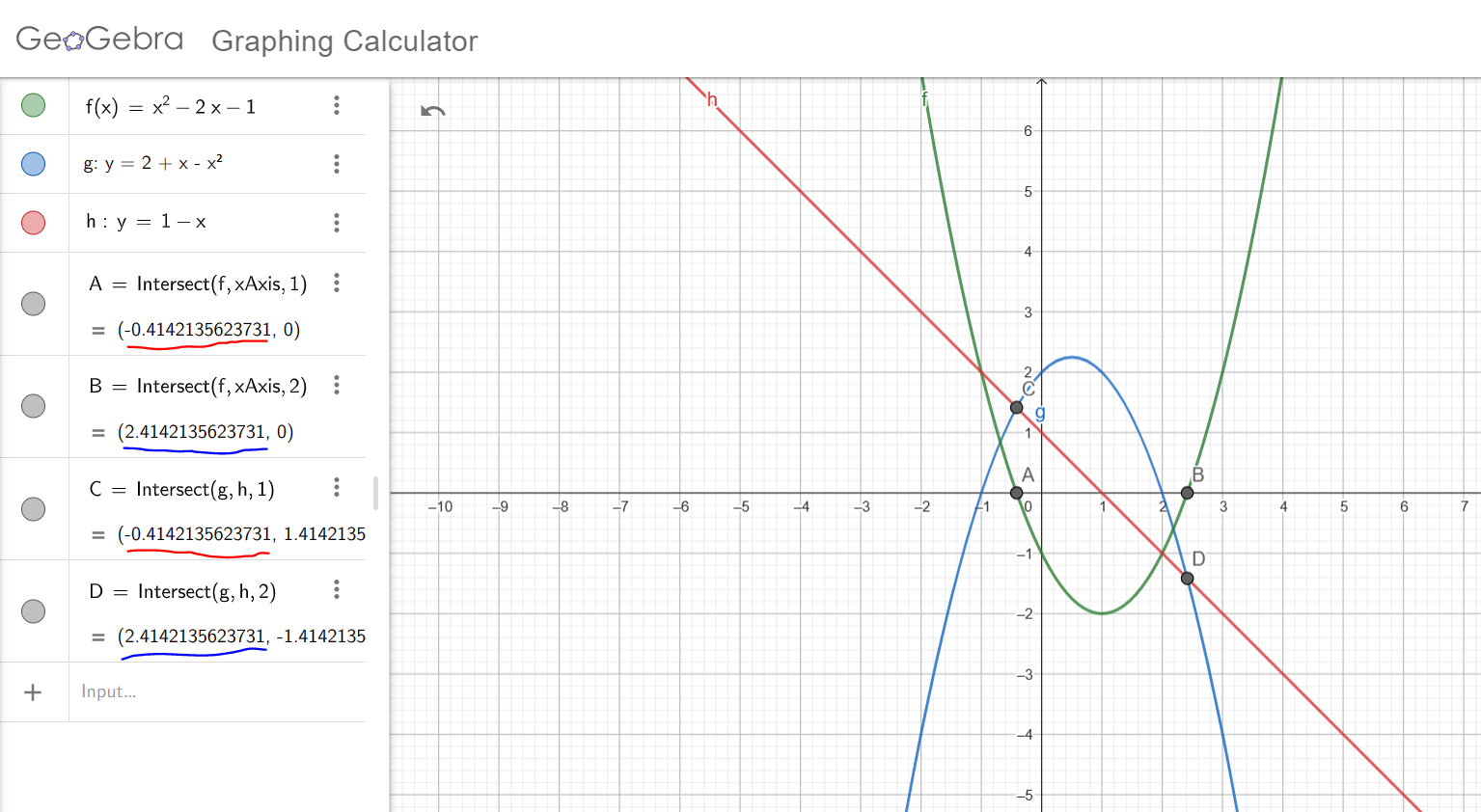
(3.) NSC Given: $f(x) = x^3 - 2x^2 - 7x - 4$
(3.1) Write down the y-intercept of f
(3.2) Show that x - 4 is a factor of f
(3.3) Determine the x-intercepts of f
(3.4) Determine the coordinates of the turning points of f
(3.5) Sketch the graph of f on the ANSWER SHEET provided. Clearly show ALL the intercepts with the axes and the turning points.
(3.6) Determine the value(s) of x for which the graph of f is decreasing.
$ f(x) = x^3 - 2x^2 - 7x - 4 \\[3ex] (3.1) \\[3ex] f(0) = 0^3 - 2(0)^2 - 7(0) - 4 \\[3ex] = 0 - 0 - 0 - 4 \\[3ex] = -4 \\[3ex] y-intercept = (0, -4) \\[3ex] (3.2) \\[3ex] Factor:\;\; x - 4 \\[3ex] Zero:\;\; x - 4 = 0 \\[3ex] x = 4 \\[3ex] f(4) = 4^3 - 2(4)^2 - 7(4) - 4 \\[3ex] = 64 - 2(16) - 28 - 4 \\[3ex] = 64 - 32 - 28 - 4 \\[3ex] = 0 \\[3ex] (3.3) \\[3ex] f(x) = 0 \\[3ex] x^3 - 2x^2 - 7x - 4 = 0 \\[5ex] 1st\;\;Factor:\;\; x - 4 \\[3ex] \begin{array}{c|c} & x^2 + 2x + 1 \\ \hline x - 4 & x^3 - 2x^2 - 7x - 4 \\ &-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ &x^3 - 4x^2~~~~~~~~~~~~~~~~ \\ \hline &~~2x^2 - 7x \\ &-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ &~~2x^2 - 8x \\ \hline &~~~~~~~~~~~~~~~~~~x - 4 \\ &-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ &~~~~~~~~~~~~~~~~~~x - 4 \\ \hline &~~~~~~~~~~~~~~~~~~0 \\[5ex] \end{array} \\[5ex] Quotient = x^2 + 2x + 1 \\[3ex] x^2 + 2x + 1 = 0 \\[3ex] (x + 1)(x + 1) = 0 \\[3ex] x + 1 = 0 \\[3ex] x = -1\;(repeated) \\[3ex] x-intercepts = (4, 0),\;\;(-1, 0),\;\;and\;\;(-1, 0) \\[3ex] (3.4) \\[3ex] f'(x) = 3x^2 - 4x - 7 \\[3ex] f'(x) = 0 \\[3ex] \implies \\[3ex] 3x^2 - 4x - 7 = 0 \\[3ex] 3x^2 + 3x - 7x - 7 = 0 \\[3ex] 3x^2 + 3x - 7x - 7 = 0 \\[3ex] 3x(x + 1) - 7(x + 1) = 0 \\[3ex] (x + 1)(3x - 7) = 0 \\[3ex] x + 1 = 0 \;\;\;OR\;\;\; 3x - 7 = 0 \\[3ex] x = -1 \;\;\;OR\;\;\; 3x = 7 \\[3ex] x = -1 \;\;\;OR\;\;\; x = \dfrac{7}{3} \\[5ex] Critical\;\;Values: x = -1 \;\;\;OR\;\;\; x = \dfrac{7}{3} \\[5ex] f(-1) = (-1)^3 - 2(-1)^2 - 7(-1) - 4 \\[3ex] = -1 - 2(1) + 7 - 4 \\[3ex] = -1 - 2 + 7 - 4 \\[3ex] = 0 \\[3ex] f\left(\dfrac{7}{3}\right) = \left(\dfrac{7}{3}\right)^3 - 2\left(\dfrac{7}{3}\right)^2 - 7\left(\dfrac{7}{3}\right) - 4 \\[5ex] = \dfrac{343}{27} - 2\left(\dfrac{49}{9}\right) - \dfrac{49}{3} - 4 \\[5ex] = \dfrac{343}{27} - \dfrac{98}{9} - \dfrac{49}{3} - 4 \\[5ex] = \dfrac{343 - 294 - 441 - 108}{27} \\[5ex] = -\dfrac{500}{27} \\[5ex] Turning\;\;Points:\;\; (-1,0) \;\;\;AND\;\;\; \left(\dfrac{7}{3},-\dfrac{500}{27}\right) \\[5ex] Turning\;\;Points:\;\; (-1,0) \;\;\;AND\;\;\; (2.333, -18.519) \\[5ex] $ (3.5)
The graph of f is:
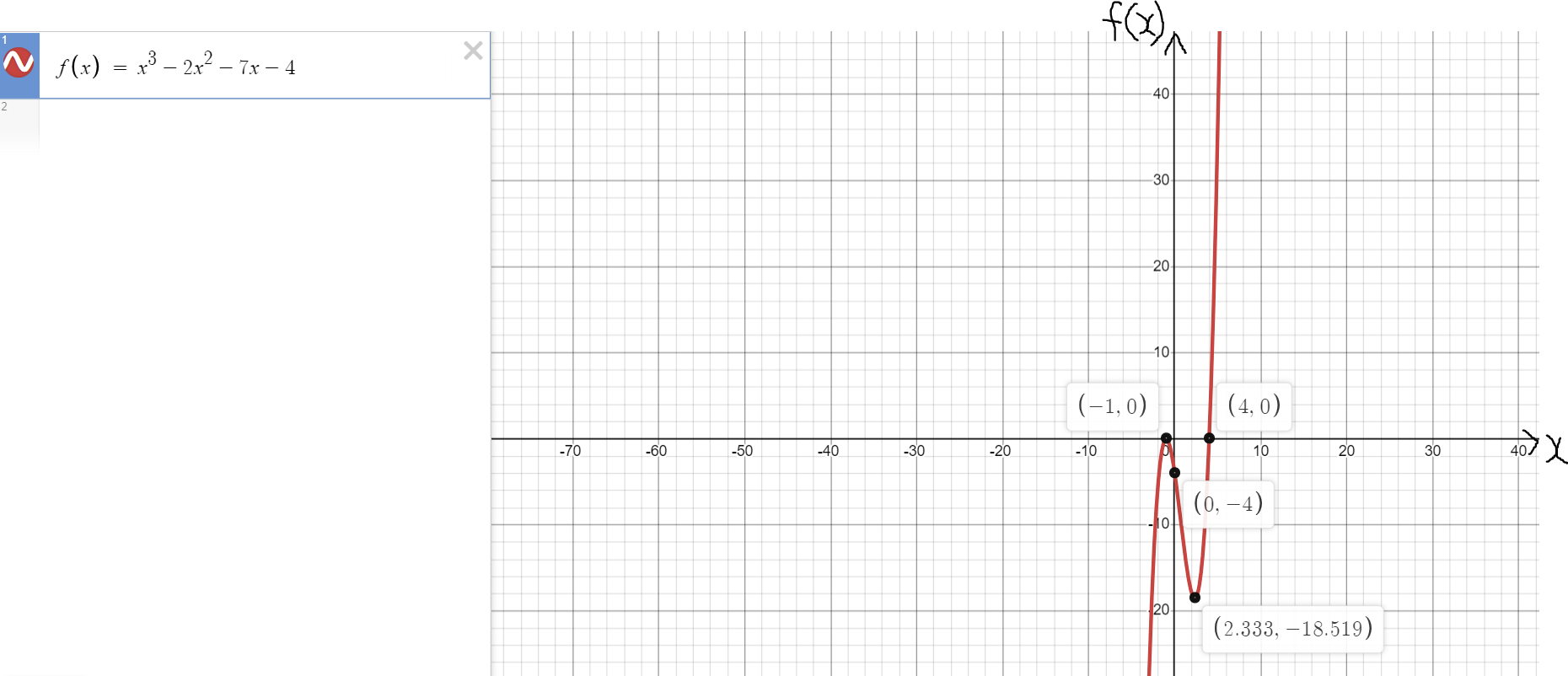
$ (3.6) \\[3ex] x \downarrow \;\;for\;\; \left(-1, \dfrac{7}{3}\right) $
(3.1) Write down the y-intercept of f
(3.2) Show that x - 4 is a factor of f
(3.3) Determine the x-intercepts of f
(3.4) Determine the coordinates of the turning points of f
(3.5) Sketch the graph of f on the ANSWER SHEET provided. Clearly show ALL the intercepts with the axes and the turning points.
(3.6) Determine the value(s) of x for which the graph of f is decreasing.
$ f(x) = x^3 - 2x^2 - 7x - 4 \\[3ex] (3.1) \\[3ex] f(0) = 0^3 - 2(0)^2 - 7(0) - 4 \\[3ex] = 0 - 0 - 0 - 4 \\[3ex] = -4 \\[3ex] y-intercept = (0, -4) \\[3ex] (3.2) \\[3ex] Factor:\;\; x - 4 \\[3ex] Zero:\;\; x - 4 = 0 \\[3ex] x = 4 \\[3ex] f(4) = 4^3 - 2(4)^2 - 7(4) - 4 \\[3ex] = 64 - 2(16) - 28 - 4 \\[3ex] = 64 - 32 - 28 - 4 \\[3ex] = 0 \\[3ex] (3.3) \\[3ex] f(x) = 0 \\[3ex] x^3 - 2x^2 - 7x - 4 = 0 \\[5ex] 1st\;\;Factor:\;\; x - 4 \\[3ex] \begin{array}{c|c} & x^2 + 2x + 1 \\ \hline x - 4 & x^3 - 2x^2 - 7x - 4 \\ &-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ &x^3 - 4x^2~~~~~~~~~~~~~~~~ \\ \hline &~~2x^2 - 7x \\ &-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ &~~2x^2 - 8x \\ \hline &~~~~~~~~~~~~~~~~~~x - 4 \\ &-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ &~~~~~~~~~~~~~~~~~~x - 4 \\ \hline &~~~~~~~~~~~~~~~~~~0 \\[5ex] \end{array} \\[5ex] Quotient = x^2 + 2x + 1 \\[3ex] x^2 + 2x + 1 = 0 \\[3ex] (x + 1)(x + 1) = 0 \\[3ex] x + 1 = 0 \\[3ex] x = -1\;(repeated) \\[3ex] x-intercepts = (4, 0),\;\;(-1, 0),\;\;and\;\;(-1, 0) \\[3ex] (3.4) \\[3ex] f'(x) = 3x^2 - 4x - 7 \\[3ex] f'(x) = 0 \\[3ex] \implies \\[3ex] 3x^2 - 4x - 7 = 0 \\[3ex] 3x^2 + 3x - 7x - 7 = 0 \\[3ex] 3x^2 + 3x - 7x - 7 = 0 \\[3ex] 3x(x + 1) - 7(x + 1) = 0 \\[3ex] (x + 1)(3x - 7) = 0 \\[3ex] x + 1 = 0 \;\;\;OR\;\;\; 3x - 7 = 0 \\[3ex] x = -1 \;\;\;OR\;\;\; 3x = 7 \\[3ex] x = -1 \;\;\;OR\;\;\; x = \dfrac{7}{3} \\[5ex] Critical\;\;Values: x = -1 \;\;\;OR\;\;\; x = \dfrac{7}{3} \\[5ex] f(-1) = (-1)^3 - 2(-1)^2 - 7(-1) - 4 \\[3ex] = -1 - 2(1) + 7 - 4 \\[3ex] = -1 - 2 + 7 - 4 \\[3ex] = 0 \\[3ex] f\left(\dfrac{7}{3}\right) = \left(\dfrac{7}{3}\right)^3 - 2\left(\dfrac{7}{3}\right)^2 - 7\left(\dfrac{7}{3}\right) - 4 \\[5ex] = \dfrac{343}{27} - 2\left(\dfrac{49}{9}\right) - \dfrac{49}{3} - 4 \\[5ex] = \dfrac{343}{27} - \dfrac{98}{9} - \dfrac{49}{3} - 4 \\[5ex] = \dfrac{343 - 294 - 441 - 108}{27} \\[5ex] = -\dfrac{500}{27} \\[5ex] Turning\;\;Points:\;\; (-1,0) \;\;\;AND\;\;\; \left(\dfrac{7}{3},-\dfrac{500}{27}\right) \\[5ex] Turning\;\;Points:\;\; (-1,0) \;\;\;AND\;\;\; (2.333, -18.519) \\[5ex] $ (3.5)
The graph of f is:

$ (3.6) \\[3ex] x \downarrow \;\;for\;\; \left(-1, \dfrac{7}{3}\right) $
(4.) JAMB If x + 2 and x − 1 are factors of the expression $lx + 2kx^2 + 24$, find the
values of l and k
$ A.\;\; l = -6,\;\;\;k = -9 \\[3ex] B.\;\; l = -2,\;\;\;k = 1 \\[3ex] C.\;\; l = -2,\;\;\;k = -1 \\[3ex] D.\;\; l = 0,\;\;\;k = 1 \\[3ex] E.\;\; l = 6,\;\;\;k = 0 \\[3ex] $
$ f(x) = lx^3 + 2kx^2 + 24 \\[3ex] 1st\;\;Factor:\;\; x + 2 \\[3ex] 1st:\;\;Zero:\;\; x + 2 = 0 \\[3ex] x = -2 \\[3ex] f(-2) = l(-2)^3 + 2k(-2)^2 + 24 \\[3ex] = -8l + 8k + 24 \\[3ex] f(-2) = 0 ...Factor\;\;Theorem \\[3ex] \implies \\[3ex] -8l + 8k + 24 = 0 \\[3ex] -l + k + 3 = 0 \\[3ex] -l + k = -3...eqn.(1) \\[3ex] 2nd\;\;Factor:\;\; x - 1 \\[3ex] 2nd:\;\;Zero:\;\; x - 1 = 0 \\[3ex] x = 1 \\[3ex] f(1) = l(1)^3 + 2k(1)^2 + 24 \\[3ex] = l + 2k + 24 \\[3ex] f(1) = 0 ...Factor\;\;Theorem \\[3ex] \implies \\[3ex] l + 2k + 24 = 0 \\[3ex] l + 2k = -24 \\[3ex] l + 2k = -24...eqn.(2) \\[3ex] eqn.(1) + eqn.(2) \implies \\[3ex] 3k = -27 \\[3ex] k = -\dfrac{27}{3} \\[5ex] k = -9 \\[3ex] Substitute\;\;k = -9\;\;into\;\;eqn.(2) \\[3ex] l + 2(-9) = -24 \\[3ex] l - 18 = -24 \\[3ex] l = -24 + 18 \\[3ex] l = -6 \\[3ex] l = -6,\;\;\;k = -9 $
$ A.\;\; l = -6,\;\;\;k = -9 \\[3ex] B.\;\; l = -2,\;\;\;k = 1 \\[3ex] C.\;\; l = -2,\;\;\;k = -1 \\[3ex] D.\;\; l = 0,\;\;\;k = 1 \\[3ex] E.\;\; l = 6,\;\;\;k = 0 \\[3ex] $
$ f(x) = lx^3 + 2kx^2 + 24 \\[3ex] 1st\;\;Factor:\;\; x + 2 \\[3ex] 1st:\;\;Zero:\;\; x + 2 = 0 \\[3ex] x = -2 \\[3ex] f(-2) = l(-2)^3 + 2k(-2)^2 + 24 \\[3ex] = -8l + 8k + 24 \\[3ex] f(-2) = 0 ...Factor\;\;Theorem \\[3ex] \implies \\[3ex] -8l + 8k + 24 = 0 \\[3ex] -l + k + 3 = 0 \\[3ex] -l + k = -3...eqn.(1) \\[3ex] 2nd\;\;Factor:\;\; x - 1 \\[3ex] 2nd:\;\;Zero:\;\; x - 1 = 0 \\[3ex] x = 1 \\[3ex] f(1) = l(1)^3 + 2k(1)^2 + 24 \\[3ex] = l + 2k + 24 \\[3ex] f(1) = 0 ...Factor\;\;Theorem \\[3ex] \implies \\[3ex] l + 2k + 24 = 0 \\[3ex] l + 2k = -24 \\[3ex] l + 2k = -24...eqn.(2) \\[3ex] eqn.(1) + eqn.(2) \implies \\[3ex] 3k = -27 \\[3ex] k = -\dfrac{27}{3} \\[5ex] k = -9 \\[3ex] Substitute\;\;k = -9\;\;into\;\;eqn.(2) \\[3ex] l + 2(-9) = -24 \\[3ex] l - 18 = -24 \\[3ex] l = -24 + 18 \\[3ex] l = -6 \\[3ex] l = -6,\;\;\;k = -9 $